Група №6 23.03.2020
Тема уроку:
Правила диференціювання
І. Актуалізація опорних знань
1. Розв’язати завдання
|
Варіант 1
|
Варіант 2
|
|
Функцію задано формулою
|
|
|
f(x) = 4 - 3x2
|
f(х) = 6 - 5х2
|
|
1) користуючись означенням, знайдіть похідну
функції;
2) знайдіть значення похідної функції в точці
х0 = 2;
3) знайдіть кутовий коефіцієнт дотичної до
графіка функції в точці х0 = —1
|
|
Відповіді
Варіант 1. 1) -6х; 2) -12; 3) 6.
Варіант 2. 1) -10х; 2) -20; 3) 10.
2. Подайте
у вигляді степеня:
3. Обчисліть f(х0), якщо:
ІІ. Вивчення нового
матеріалу
Робота з підручником ___ст.
138 -139___________________________
Заповніть порожні місця
в таблиці.
Похідні елементарних
функцій
|
Функції
|
Стала функція
|
Степенева функція
|
Окремі випадки степеневої функції
|
Тригонометричні функції
|
|||||
|
n = 1
|
n = -1
|
n = 1/2
|
|||||||
|
f(x)
|
C
|
xn
|
x
|
1/x
|
√X
|
sin x
|
cos x
|
tg x
|
ctg x
|
|
Похідні f'(x)
|
|
|
|
|
|
|
|
|
|
План
вивчення теми
1. Правила диференціювання:
• (Cu)' = C ∙ u', де C — сталий множник;
• похідна суми: (u + v)' = u' + v';
• похідна добутку: (uv)' = u'v + uv';
• похідна частки:
за умови, що v ≠ 0.
ІІІ. Застосування знань і вмінь
1) Знайдіть похідну функції:
2) Чому дорівнює f'(x), якщо:
ІV. Домашнє завдання
Вивчити ст.138
-139, розв’язати №435, 444.


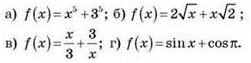
Немає коментарів:
Дописати коментар