25.10.2021 ГРУПА №4 ГЕОМЕТРІЯ
Тема уроку: Контрольна робота за темою "Паралельність прямих і площин у просторі"
1. Виконати роботу на двойному листку (копію прислати на вайбер, після закінчення карантину здати)
Якій із указаних площин належить точка Р?
(див. малюнок)
Яка з наведених фігур може бути лінією перетину двох площин?
Через яку з фігур можна провести безліч площин?
Як називаються прямі, які не перетинаються і лежать в одній площині?
Дві площини називаються паралельними, якщо вони:
На рисунку точка А середина відрізка РК, АВ ∥ СD, BC ∥ AD, BC ∥ PM, CD ∥ NK. Знайдіть РМ і NK, якщо СD=16см, ВС=8см.
(Розв"язання задачі запишіть на аркуші. Без розв"язання правильна відповідь не зараховується)
Дві паралельні площини α і β перетинають сторони ВА кута АВС в точках D і D1, а сторону ВС – відповідно в точках Е і Е1. Знайдіть довжину відрізка DE, якщо BD=12 см, BD1=18 см, D1Е1=54 см.
(Розв"язання задачі запишіть на аркуші. Без розв"язання правильна відповідь не зараховується)
Дано куб АВСДА1В1С1Д1.Укажіть площину, паралельну прямій С1Д1.
Укажіть правильне твердження:
А Через три точки завжди можна провести лише одну площину
Б Якщо дві точки прямої належать площині, то пряма перетинає цю площину
В Якщо А, В, С – спільні точки двох різних площин, то вони лежать на одній прямій
Г Через три точки завжди можна провести безліч площин
Через кінці вдрізка АВ і його середину С проведено пралельні прямі, що перетинають площину α в точках А1, В1 і С1 відповідно. Відрізок АВ не перетинає площину α. Знайдіть довжину вдрізка ВВ1, якщо АА1=10 см, СС1 = 3⋅ВВ1. Розв'язок обгрунтувати.
(Розв"язання задачі запишіть у зошиті. Без розв"язання правильна відповідь не зараховується)
Користуючись зображенням куба АВСDA1B1C1D1, вкажіть паралельні площини, які проведені через мимобіжні прямі АВ і СС1
варіанти відповідей
(АВС) i (A1D1C1)
Через точку поза площиною можна провести …
Дві сторони трикутника паралельні деякій площині. Тоді третя сторона
трикутника ...
Через точку К проведено прямі А1А2 і В1В2 , що перетинають паралельні площини α і β у точках А1, А2, В1 і В2 відповідно. Знайдіть КВ1, якщо А1А2=4, КВ2=15, а КА1=В1В2.
(Розв"язання задачі запишіть у зошиті. Без розв"язання правильна відповідь не зараховується)
Точка К лежить між паралельними площинами α і β. Через точку К проведено прямі А1А2 і В1В2, які перетинають площини α і β у точках А1, А2, В1 і В2 відповідно. Знайдіть А1А2, якщо А1К=2см, В1К=5см, В1В2=12см .
(Розв"язання задачі запишіть у зошиті. Без розв"язання правильна відповідь не зараховується)
Як розташований у просторі трикутник відносно площини проекції, якщо внаслідок паралельного проектування він проектується у відрізок?
Оберіть варіанти відповіді, щоб твердження було правильним: "Унаслідок паралельного проектування фігур на площину зберігається ...
Які, з наведених фігур, можуть бути паралельною проекцією паралелограма?
Укажіть правильне твердження:
А Через три точки завжди можна провести лише одну площину
Б Якщо дві точки прямої належать площині, то пряма перетинає цю площину
В Якщо А, В, С – спільні точки двох різних площин, то вони лежать на одній прямій
Г Через три точки завжди можна провести безліч площин
Виберіть правильне твердження
Сторона АС трикутника АВС лежить у площині α . Через точку М, яка є серединою сторони АВ, проведено площину β,, паралельну площині α і яка перетинає ВС в точці К. Знайдіть МК, якщо АС=10см.
ТЕМА УРОКУ: Елементи комбінаторики. Комбінаторні правила суми та добутку
1. Передивіться відео урок за посиланням
https://www.youtube.com/watch?v=NORqFoG5pW0
2. Законспектувати в зошиті матеріал за посиланням
3. Розберіть задачі з розв'язками
Задача 1. Скількома способами можна пошити двокольоровий прапор зі смужками однакової ширини, якщо є матеріал восьми різних кольорів?
Розв'язання:Відповідь на завдання знаходять через розміщення з 8 по 2, оскільки один колір можна вибрати 8 способами, другий (8-1)=7 способами.
n=A82=8*7=56.
Задача 2. Скільки різних двоцифрових чисел можна скласти, використовуючи цифри 1, 2, 3, 4, 5, 6 якщо цифри:
1) повторюються;
2) не повторюються?
Розв'язання: Якщо цифри повторюються, то на перше місце можна поставити одну з 6, на друге також любу з 6, тому кількість двоцифрових чисел з повтореннями рівна
n=6*6=36.
2) Якщо цифри не повторюються, то на друге місце можна поставити всі цифри крім тої, що на першому місці, тому кількість рівна
n=6*5=30.
Але є задачі на цифри, які в такий спосіб не розв'язати.
Задача 3. Скільки трицифрових чисел можна скласти з цифр від 0 до 5, якщо:
1) цифри не повторюються;
2) отримане число має бути непарним;
3) число має бути кратним 5.
Розв'язання: Слід зауважити, що на перше місце не можна ставити 0, тому тут може бути одна з 5 цифр {1,2,3,4,5}. На другому місці 1 з 5 цифр, оскільки одну використали, зате добавився {0}, на третьому одна з 4.
Тому кількість різних трицифрових чисел рівна
N=5*5*4=100.
2) Якщо число непарне, то на третьому місці повинні стояти цифри 1,3,5
Тобто група має вигляд ХХ{1,3,5}, тоді на перші два місця потрібно вибрати одну з 5 цифр, включаючи 0. Тому на перше місце можна поставити 4 цифри без нуля і на друге одну з 4, включаючи 0.
Тому кількість таких цифр рівна
N1=4*4*3=48.
3) Число має бути кратним 5, тому вкінці повинно закінчуватися на 0 або на 5.
Якщо на 0, то на перші два місця потрібно ставити цифри {1,2,3,4,5}. Кількість способів це зробити рівна m1=5*4=20.
Якщо закінчується на 5, то на перше місце ставимо {1,2,3,4} без 0, на друге три з цієї групи+0, тому кількість різних чисел рівна m2=4*4=16.
Якщо маємо "або" то використовуємо комбінаторне додавання
N=m1+m2=36.
Завжди розмірковуйте, які можливі випадки, як можна розгалузити випадки. Для цього потрібно навчитися ставити правильні питання: Якщо ...?
Повірте розуміння прийде з практикою, тому більше розв'язуйте самостійно.
Задача 4. Дитині подарували набір з 10 цифр та 26 букв. Скількома способами можна скласти набір із:
1) двох букв або двох цифр;
2) двох букв і двох цифр.
Розв'язання: Дві букви з 26 можна вибрати розміщеннями з 26 по 2:
m1=A262=26!/24!=26*25=650.
Аналогічна схема вибору двох цифр з 10:
m2=A102=10!/8!=10*9=90.
1) "Або" в першій умові означає, що слід застосувати правило суми для обчислення кількості груп з 2 букв або 2 цифр:
N=m1+m2=650+90=740.
2) Кількість наборів з двох букв "і" двох цифр знаходимо за правилом добутку:
N1=m1*m2=650*90=58500.
Задача 5. На паралельних прямих а і в розміщено 10 і 7 точок відповідно. Скільки існує відрізків, що з'єднують точки прямих а і в?
Розв'язання: Нехай а1, а2, …, а10 – точки на прямій а,
в1, в2, …,в7— точки на прямій в.
Для кожної точки аі матимемо 7 відрізків, що сполучають цю точку з точками прямої в.
Кожному відрізку відповідатиме пара (аі ,вj).
За формулою комбінаторного множення кількість пар рівна
N=n·m.
Задача 6. Розклад одного дня містить 6 уроків. Визначити кількість таких розкладів при
виборі із 11 дисциплін.
Розв'язання: Для нас важливий порядок предмету в розкладі, томі якщо математика буде першим, а хімія - третім уроком, то це два різні розклади, і так для всіх 11 предметів. Тому тут не слід використовувати комбінації, тільки розміщення.
Тому кількість різних розкладів рівна:
A116=11!/(11-6)!=11*10*9*8*7*6=332640.
Задача 7. Скількома способами модна вибрати двох чергових із групи 17 чоловік?
Розв'язання: Тут неважливий порядок входження школярів в групу, а лише кількість різних груп, тому застосовуємо формулу комбінацій С
з 17 по 2:
C172=17!/(17-2)!/2!=17*16/2=136.
Отже, можемо скласти 136 різних пар з двох чергових.
Задача 8.В ящику є 10 деталей. Скількома способами можна вибрати 3 деталі?
Розв'язання: Нам неважливий порядок вибору, головне щоб в наборі було три деталі. Кількість різних наборів знаходимо через комбінації з 10 по 3:
C103=10!/(10-3)!/3!=10*9*8/6=120.
Задача 9. Група з 7 осіб займає місця за круглим столом випадковим чином. Яка ймовірність того, що дві певні особи сядуть поруч?
Розв'язання: Кількість всіх можливих перестановок з 7 осіб рівна n=7!, кількість сприятливих розміщень
m=2*7*5!, тому ймовірність розсадити 7 осіб, щоб дві певні особи були поруч рівна частці:
P=m/n=2*7/(7*6)=1/3.
___________________________________________________________________________________________________
_________________________-_________________________________________________________________________
25.10.2021 ГРУПА № 6 факультатив
Тема уроку: Розв'язування задач з теми Квадратні рівняння"
1. Передивіться відео урок за посиланням
https://www.youtube.com/watch?v=UylSG0MzcrM
2. Розв'язати завдання в зошиті
1. (0,5 бала) Розв’язати рівняння х2+5х-6=0.
а) -1;6; б) 1;-6; в) 2;-3; г) -2;3.
2. (0,5 бала) Розв’язати рівняння(х-6)(х+6)=-11.
а) 5; б) 6; в) -6;6; г) -5; 5.
3.(0,5 бала) Чому дорівнює сума коренів рівняння х2-7х+12=0.
а) 7; б) - 7; в) 12; г) -12
4. (0,5 бала) Рівняння х2+кх+р=0 має корені 2 і 4. Знайти к.
а) 8; б) -8; в) 6; г)-6.
5.(За кожну відповідність 0,5 бала) Установити відповідність між виразами
( 1-4) і їх розкладами на множники ( А-Д).
| 1. | 12х2-12х+3 | а. | (х-1)(х-8) |
| 2. | х2-х-6 | б. | (х-3)(х+2) |
| 3. | х2-9х+8 | в. | (х+3)(3х-2) |
| 4. | 3х2+7х-6 | г. | 3(2х-1)2 |
| д. | (х-3)(3х+2) |
6. ( 1 бал) Розв’язати рівняння: х4-13х2+36=0.
7. ( 2 бали ) Одна із сторін прямокутника на 5см менша за іншу, його площа 84см. Знайти сторони прямокутника.
________________________________________________________________
________________________________________________________________
25.10.2021 ГРУПА №7 ФАКУЛЬТАТИВ
Тема уроку: Обчислення площ трапеції
1. Передивіться відео урок за посиланням
https://www.youtube.com/watch?v=0ZXbQhOMoqY
2. Проаналізуйте задачі
Площа криволінійної трапеції
Площа криволінійної трапеції, обмеженої графіком неперервної додатної на відрізку 
функції 
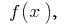віссю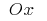 
і прямими 
і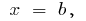 
дорівнює
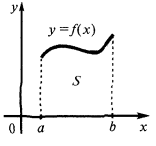
Приклад.Обчислити площу фігури, обмеженої лініями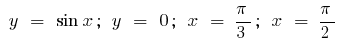 
Зображуючи ці лінії, одержуємо криволінійну трапецію
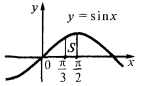
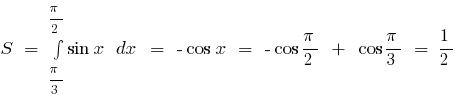
Площа фігури обмеженої графіками двох функцій і прямими і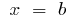 
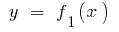Якщо на заданому відрізку неперервні функції 
і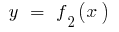 
мають ту властивість, що 
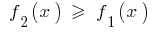для всіх 
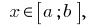то
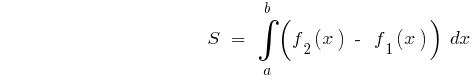
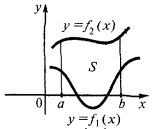
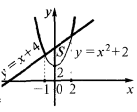
Приклад.Обчислити площу фігури, обмеженої лініями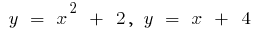 
Зобразимо задані лінії і абсциси їх точок перетину.
Абсциси точок перетину: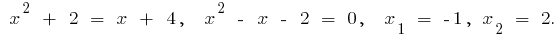 
Тоді за формулою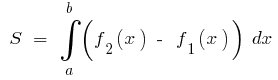 
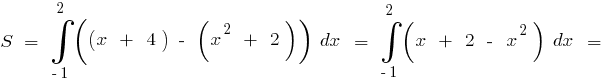
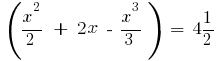
Немає коментарів:
Дописати коментар