09.11.2021 математика в групі №7,
в групах № 4 і №9 факультатив (плани уроків нижче)
________________________________________________________
09.11.2021 група №7 алгебра
Тема уроку: Контрольна робота з теми "Елементи комбінаторики, теорії ймовірностей і математичної статистики"
1. Розв'язати задачі
Варіант 1 1.(1б) У коробці лежать 12 кольорових олівців, з яких 2 – сині. Яка ймовірність того, що навмання взятий із коробки олівець буде синім? а) 2.(1б) Знайти середнє значення вибірки: 2; 4; 6; 6; 6; 7; 9; 9; 11. а) 6; б) 6 3.(1б) Скільки чисел у ряду, якщо його медіаною є п’ятнадцятий член? а) 14; б) 15; в) 28; г) 29. 4.(1б) Скількома способами можна сформувати комісію з трьох осіб, яких треба вибрати з 4 претендентів? а) 3; б) 4; в) 6; г) 12. 5.(1б) У класній кімнаті знаходилось 20 дівчат і 5 хлопців. Двоє учнів вийшли один за одним з кімнати. Яка ймовірність того, що обидва учні були хлопцями? а) 6.(1б) Скільки трицифрових чисел з різними цифрами можна записати, використовуючи цифри 1, 2, 3, 4, 5, 6? а) 120; б) 720; в) 20; г) 216. 7.(1б) Обчислити: а) 8. (2б) Розв’язати рівняння: 9.(2б) Дано вибірку: 5; 8; 4; 5; 2; 6; 5; 4; 2 . Знайти Ії розмах, моду, медіану і середнє значення. Побудувати полігон частот. 10.(1б) У лотереї з 50 білетів 8 виграшних. Яка ймовірність того, що серед п’яти навмання вибраних білетів два будуть виграшними? | Варіант 2 1.(1б) У класі 27 учнів, із них три – на ім’я Максим. Яка ймовірність того, що учня, якого навмання викликали до дошки, зватимуть Максим? а) 2.(1б) Знайти середнє значення вибірки: 6; 12; 6; 7; 8; 1; 8; 2; 13; 8; 10. а) 7 3.(1б) Скільки чисел у ряду, якщо його медіаною є тринадцятий член? а) 25; б) 13; в) 26; г) 27. 4.(1б) У бригаді робітників з 8 осіб треба сформувати групу з 3 осіб, які мають їхати у відрядження. Скількома способами це можна зробити? а)56; б) 48; в) 36; г) 28. 5.(1б) У кімнаті знаходилось 14 дітей, половина з яких – дівчата. Четверо дівчат вийшло з кімнати. Яка ймовірність того, що наступна дитина, яка вийде з кімнати, буде дівчиною? а) 6.(1б) Скільки двоцифрових чисел з різними цифрами можна записати, використовуючи цифри 1, 2, 3, 4, 5, 6? а) 60; б) 30; в) 48; г) 36. 7.(1б) Обчислити: а) 8. (2б) Розв’язати рівняння: 9.(2б) Дано вибірку: 7; 5; 4; 6; 4; 3; 8; 5; 4 . Знайти Ії розмах, моду, медіану і середнє значення. Побудувати полігон частот. 10.(1б) В ставку плавають 14 окунів і 6 карасів. Рибак зловив 7 риб. Яка ймовірність того, що серед пійманих риб є 3 карася і 4 окуня? |
2. Розв'язати тести (додаткове завдання)
Скількома способами можна скласти список із 5 прізвищ ?
Скільки елементів повинна містити множина, щоб число перестановок було не більше 100 ?
Скоротіть дріб k! / (k-1)!
Обчисліть А84
Обчислити С53 + С54 + С55.
Із 10 троянд і 8 жоржин треба скласти букет так, щоб в ньому були 2 троянди і 3 жоржини. Скількома способами можна скласти букет ?
В скриньці лежать 12 білих і 8 червоних однакових на дотик кульок. Вийнято навмання одну кульку. Яка ймовірність того, що вона біла ?
Знайти суму моди, медіани та розмаху вибірки 5, 8, 6, 6, 2, 7, 7, 7, 4, 4, 1.
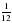 ; б)
; б) 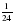 ; в)
; в) 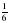 ; г)
; г) 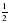 .
.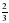 .
.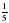 ; б)
; б) 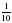 ; в)
; в) 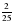 ; г)
; г)  .
.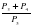 ; б)
; б)  ; в)
; в) 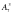 .
.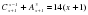 .
.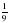 ; б)
; б)  ; в)
; в) 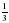 ; г)
; г) 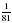 .
. ; г) 8.
; г) 8.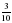 ; б)
; б) 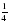 ; в)
; в) 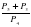 ; б)
; б) 
Немає коментарів:
Дописати коментар