16.042021 група №14 Алгебра і початки аналізу
Тема уроку: Правила диференціювання
Законспектувати в зошит і вивчити:
Правила диференціювання |
1) Сталий множник можна виносити за знак похідної. (с u(x))’ = cu’(x), (с – стала, тобто число) u(x))’ = cu’(x), (с – стала, тобто число) |
Приклад: у = 5х;
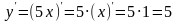 . .
y = 3x2;
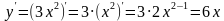 . .
2) Похідна суми (різниці) функцій, які диференціюються, дорівнює сумі (різниці) їхніх похідних. 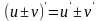
| Приклад: у = 8х2 + 5х – 4. 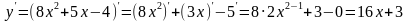 . .
| 3) Похідна добутку двох функцій, які диференціюються, дорівнює похідній першої функції помноженій на другу функцію плюс похідна другої функції помножена на першу функцію. 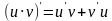
| Приклад: у = х2(x3 – 5). 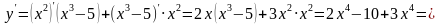
= 5x4 – 10x. 4) Похідна частки двох функцій, які диференціюються, дорівнює дробу в чисельнику, якого похідна першої функції помножена на другу функцію мінус похідна другої функції помножена на першу функцію, а в знаменнику квадрат другої функції. 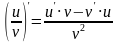
| Приклад: 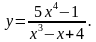
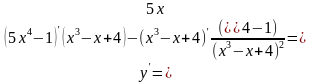
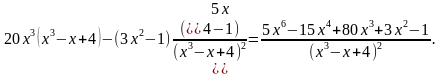
|
Рівняння дотичної до графіка функції Загальний вигляд рівняння дотичної, проведеної до графіка функції у = f(x) у точці дотику (х0; у0) 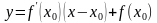
Щоб записати рівняння дотичної до графіка функції в точці з абсциссою х0 треба: 1) Знайти загальний вигляд похідної. 2) Знайти значеня похідної в точці х0. 3) Знайти значення функції в точці х0. 4) Підставити отримані числа, тобто f'(x0); x0; f(x0) у рівняння дотичної. 5) Розкрити дужки, звести подібні. 6) Записати отримане рівняння дотичної у вигляді лінійної функції. №1485 Написати рівняння дотичної до графіка даної функції в його точці з абсциссою х0. а)у = х2 – 2х ; x0 = 3. 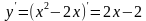 ; ;
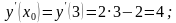
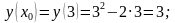
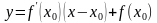 або або
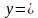 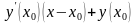 - рівняння дотичної - рівняння дотичної
у = 4(х – 3) + 3 = 4х – 12 + 3 = 4х – 9. Відповідь: у = 4х – 9. Передивіться відеоурок за посиланням: https://www.youtube.com/watch?v=-L2730ndf8A Виконати самостійно: № 434, 435, 437 ст141 підручника.
|
|
Немає коментарів:
Дописати коментар