16.09.2022     група  №2    геометрія 

Тема уроку: Перерізи циліндра і конуса площинами, паралельними основі

1. Передивіться відеоурок

https://www.youtube.com/watch?v=yFQpHNrrY8w

2. Законспектуйте взошиті

Перерізи конуса площинами

Розглянемо перерізи конуса площиною, яка проходить через вершин S конуса.

1) 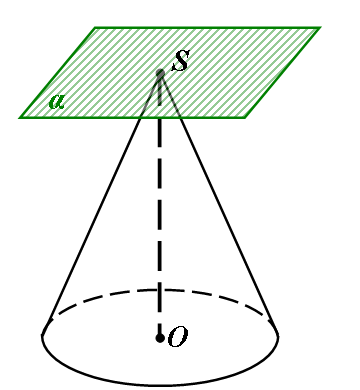  2)    

 

3)   

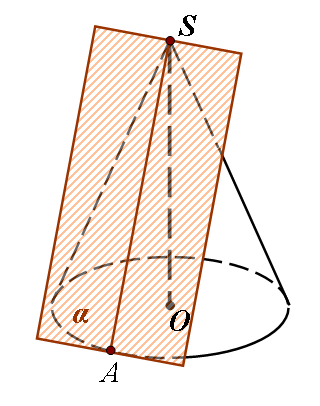
Якщо площина проходить через вершину конуса, то вона перетинає бічну поверхню або в одній точці (1), або по двом її твірним (2), або має з поверхнею одну спільну твірну, тобто дотикається до даної поверхні (3).

У другому випадку в перерізі отримаємо рівнобедрений трикутник, оскільки твірні конуса рівні. Переріз, який містить вісь конуса називається осьовим.

Розглянемо переріз площиною, яка не містить вершину конуса, а саме, паралельна основі.

 

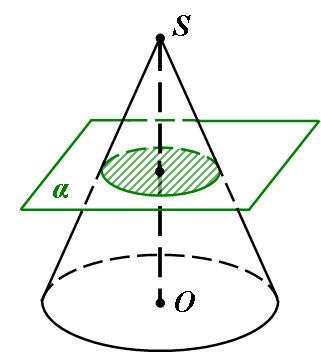
Теорема. Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню  – по колу з центром на осі конуса.

 

 

Доведення.

Нехай α – площина, паралельна площині основи конуса і перетинає конус.

Перетворення гомотетії відносно вершини конуса, яке суміщає площину α з площиною основи, суміщає переріз конуса площиною α з основою конуса. Отже, переріз конуса площиною є круг, а переріз бічної поверхні – коло з центром на осі конуса.

Теорема доведена.

 

Якщо розглянути декілька площин, які паралельні площині основи конуса і перетинають бічну поверхню, то в перерізах матимемо гомотетичні круги, центром гомотетії яких є вершина конуса, а модуль коефіцієнта гомотетії (k) дорівнює відношенню відстаней січних площин від вершини конуса.

 

Випадки розташування січної площини відносно бічної поверхні, що залишилися, можна розділити на три:

1) площина, паралельна осі поверхні;

2) площина, паралельна одній з її твірних;

3) січна площина непаралельна ні осі поверхні, ні її твірним.

В усіх цих випадках площина перетинає конічну поверхню по лініям, які в шкільному курсі геометрії не досліджуються. Це – гіпербола, парабола і еліпс. Історично ці лінії і з’явилися як перерізи конічної поверхні площиною, тому і називаються конічними перерізами. З проникненням в геометрію алгебраїчних методів дослідження, виявилося, що лінії можуть бути представлені рівняннями. Було встановлено, що конічним перерізам відповідають алгебраїчні рівняння другого порядку (прикладом може бути рівняння кола), внаслідок чого ці лінії стали називати лініями другого порядку.

     

 

 

 

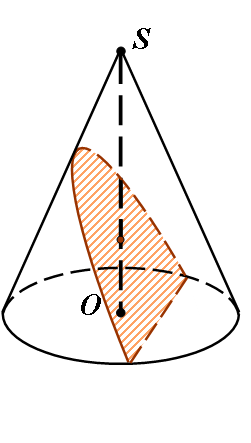
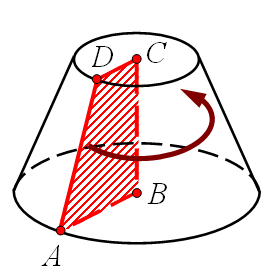
Якщо обертати прямокутну трапецію навколо прямої, що містить бічну сторону, яка перпендикулярна основам трапеції, то отримаємо тіло, яке називається зрізаним конусом.

Круги, що описуються основами трапеції, називаються основами зрізаного конуса, а відстань між ними - висотою. В нашому випадку це відрізок CB (мал.)

 

Назва «зрізаний конус» пов'язана з тим, що це тіло можна розглядати і як частину конуса, відсікаємого від нього деякого січною площиною, перпендикулярною осі конуса.

 

 

Дайте відповіді на питання:

• 1) Дати означення конуса.
• 2) Який конус називається прямим?
• 3) Дати означення основних понять: радіус конуса, твірна конуса, висота конуса.
• 4) Які перерізи конуса площинами вам відомі?Циліндром називається тіло, утворене обертанням прямокутника навколо його сторони.

  На рис. 1 зображено циліндр, утворений обертанням прямокутника ОАBO₁ навколо OO₁, OO₁ — вісь циліндра. Сторони ОА і О₁В описують рівні круги, які лежать у паралельних площинах і називаються основами циліндра. Радіуси кругів називаються радіусами циліндра. Сторона АВ описує поверхню, яка називається бічною поверхнею циліндра. Вирізки бічної поверхні, які паралельні і дорівнюють АВ, називаються твірними циліндра.

  Висотою циліндра називається відрізок, перпендикулярний до основ, кінці якого належать основам. Висота циліндра дорівнює його твірній.

  Переріз циліндра площиною, перпендикулярною до його осі,— круг, що дорівнює основі (рис. 2), а переріз площиною, паралельною осі, — прямокутник (рис. 3) або відрізок.

• Осьовий переріз — прямокутник зі сторонами, що дорівнює висоті циліндра і діаметру його основи (рис. 4).

  

  Рис. 1

  

  Рис. 2

  

• Рис. 3

• 3. Розв'яжіть задачі

• 1. Осьовим перерізом циліндра є квадрат, площа якого дорівнює 16 см². Знайдіть висоту циліндра.

• 2. Діагональ осьового перерізу циліндра дорівнює 13 см. Знайдіть радіус циліндра, якщо його висота дорівнює 5 см.

• 3. Знайдіть площу (у см²) осьового перерізу циліндра, якщо радіус циліндра і його висота відповідно дорівнюють 3 см і 8 см.

• 4. Радіус основи конуса дорівнює б см, висота — 8 см. Знайдіть твірну конуса.

• 5. Знайдіть площу осьового перерізу зрізаного конуса, якщо висота зрізаного конуса дорівнює 10 см, а радіуси основ дорівнюють 5 см і 7 см.