22.11.2022      група   № 7     (№41)    алгебра і початки аналізу

Тема уроку: Ознака сталості функції.    Достатня умова зростання (спадання)  функції.

1. Передивіться відео урок за посиланням

https://www.youtube.com/watch?v=u-433NKOLaI

2. Законспектувати в зошиті

 Функція  називається зростаючою в проміжку , якщо для будь-яких  і , що належать до цього проміжку, і таких, що  справджується нерівність .

Функція  називається спадною в проміжку , якщо для будь-яких  і , що належать до цього проміжку, і таких, що  справджується нерівність .

Як зростаючі, так і спадні функції називаються монотонними, а проміжки, в яких функція зростає або спадає, - проміжками монотонності.

Зростання і спадання функції  характеризується знаком її похідної: якщо в деякому проміжку , то функція зростає в цьому проміжку; якщо ж , то функція спадає в цьому проміжку.

Внутрішні точки області визначення функції , в яких похідна дорівнює нулю () або зазнає розриву, називаються критичними точками.

Знаходження проміжків монотонності функції можна виконувати за таким планом:

+

1. Знайти область визначення заданої функції;

2. Знайти похідну ;

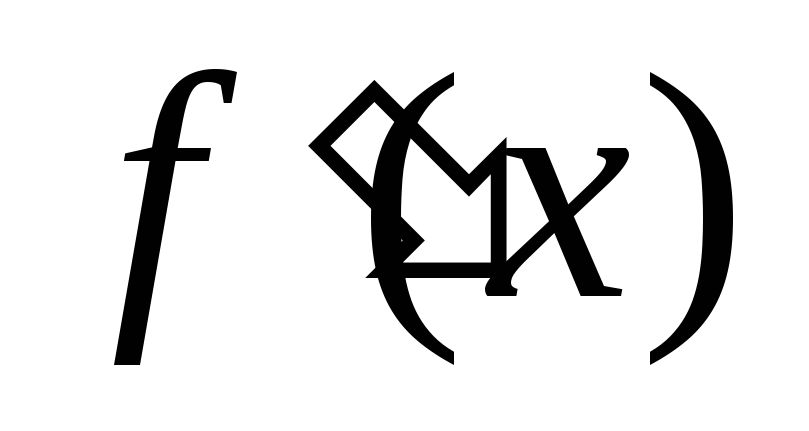3. Знайти критичні точки функції ;

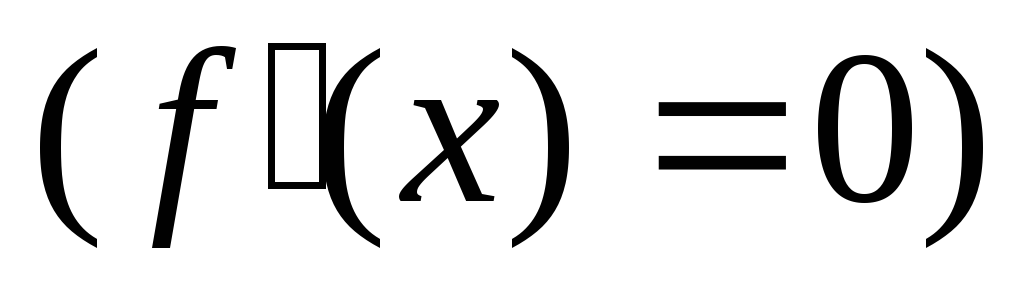4. Нанести критичні точки на область визначення функції;

5. Визначити знак похідної 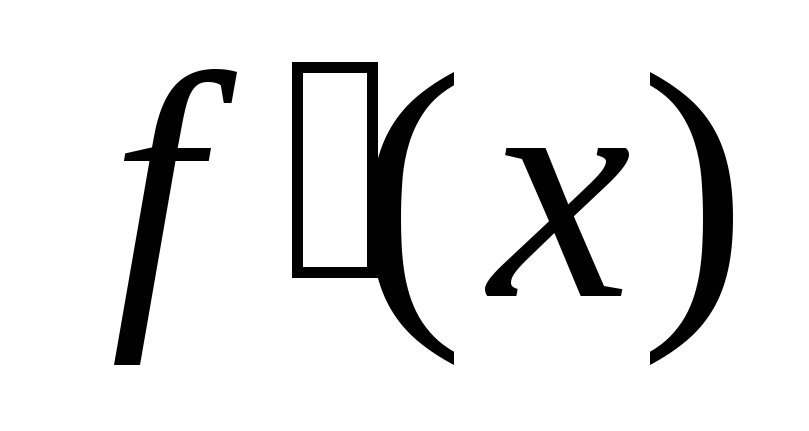 на кожному з отриманих проміжків;

6. Виписати проміжки монотонності функції.                                                    3. Розв'язати приклади

Дослідити функції на монотонність:

1) ; 2) ;

3); 4);

5); 6);

7); 8);

9); 10);

11); 12);

13); 14);

____________________________________________________________________________________________________________________________________________