24.11.2022     група   №9          алгебра і початки аналізу

Тема уроку: Властивості та графік логарифмічної функції  (№40)

1. Передивіться відеоурок

https://www.youtube.com/watch?v=tY-iPSbafOk

2. Законспектуйте і вивчіть

Показникове рівняння вигляду 3x=5 можна розв'язати за допомогою введення нового символу log3,

тоді, корінь рівняння x= log35 (логарифм числа 5 за основою 3).

Логарифмом додатного числа b за додатною і відмінною від 1 основою a 

називають показник степеня, до якого потрібно піднести число a, щоб отримати число b.

logab= c, ac=b, де  a>0,a≠1,b>0

Приклад:

1. log39= 2, оскільки 32=9

 

2. log1749= -2, оскільки (17)−2=49

 

3. Знайти x:

log2√4–√3 = x

За визначенням логарифма

(2–√)x=4–√32x2=4132x2=(22)132x2=223x2=23x=2⋅23x=43

Зверни увагу!

Для будь-якого a>0,a≠1:

 

logaa=1

loga1=0

loga(ab)=b

Приклад:

log88=1, оскільки 81=8

log251=0, оскільки 250=1

log7735=35

Логарифм з основою 10 називають десятковим логарифмом, замість log10b пишуть lgb.

Логарифм з основою е, де е - ірраціональне число, приблизно дорівнює 2,7, називають натуральним логарифмом. Замість logeb пишуть lnb.

Розглянемо деяку властивість логарифма:

alogab=b, де b>0,a>0,a≠1.

Цю рівність називають основною логарифмічною тотожністю

Приклад:

1. (13)log132=2

 

2. 17log1735=35

 

3. 8−2log85=(8log85)−2=5−2=125

 

4. 41+log45=41⋅4log45=4⋅5=20

 

5. 32−log318=32:3log318=9:18=918=12

Функцію, задану формулою y=logax (a>0,a≠1), називають логарифмічною функцією з основою a.

 

 

 

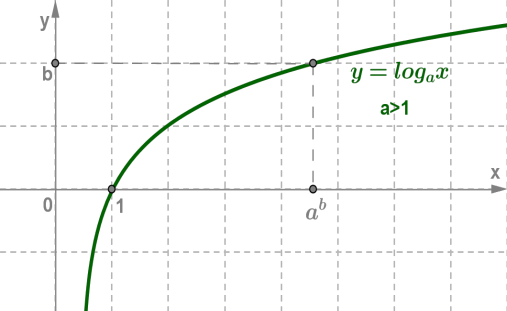
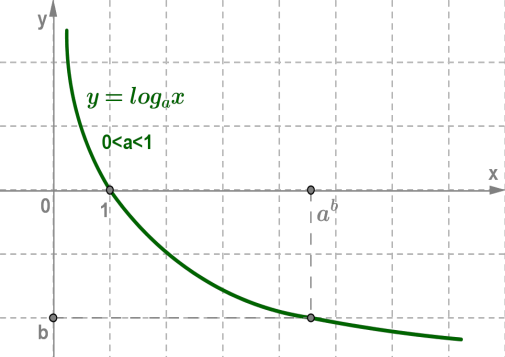
Основні властивості логарифмічної функції:

1. Область визначення логарифмічної функції — множина всіх додатних чисел.

D(f)=(0;+∞);

 

2. Множина значень логарифмічної функції — множина R всіх дійсних чисел.

E(f)=(−∞;+∞);

 

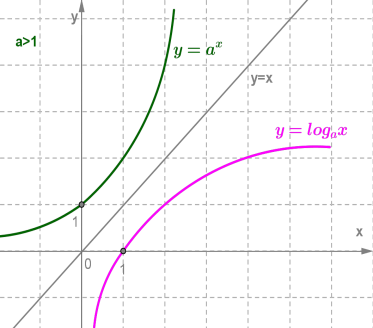
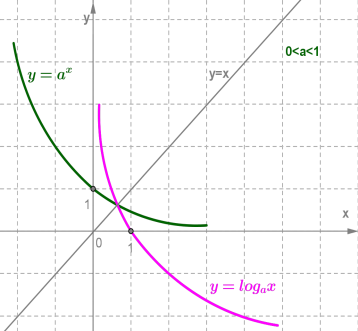
3. Логарифмічна функція на всій області визначення зростає при a>1, або спадає

 при 0<a<1.

Зверни увагу!

 Логарифмічна функція не є ні парною, ні непарною;
 не має ні найбільшого, ні найменшого значень;
 не обмежена зверху, не обмежена знизу;

Графік будь-якої логарифмічною функції y=logax проходить через точку (1;0).

Побудуємо графіки двох функцій

Приклад:

1. y=log2x, основа 2>1

x	14	12	1	2	4	8
y=log2x	−2	−1	0	1	2	3

 

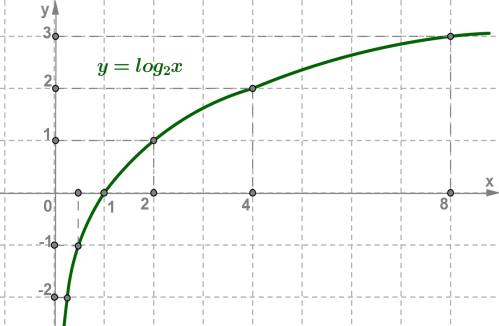
Приклад:

2. y=log13x основа 0<13<1

x	9	3	1	13	19
y=log13x	−2	−1	0	1	2

 

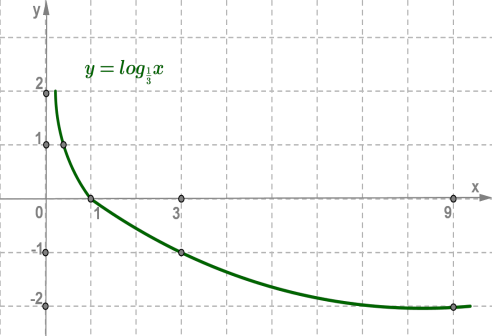
Логарифмічна функція y=logax і показникова функція y=ax, де (a>0,a≠1), взаємно обернені. Графіки цих функцій симетричні відносно прямої y=x.

 

           

3. Виконайте тести

Знайдіть log525

варіанти відповідей

 

5

 

 

2

 

 

10

 

 

20

Запитання 2

Знайдіть log232

варіанти відповідей

 

5

 

 

30

 

 

16

 

 

4

Запитання 3

Знайдіть log√39

варіанти відповідей

 

81

 

 

⅓

 

 

1

 

 

4

Запитання 4

Знайдіть log6⅙

варіанти відповідей

 

2

 

 

3

 

 

√6

 

 

-1

Запитання 5

Знайдіть lg1000

варіанти відповідей

 

10

 

 

3

 

 

30

 

 

2

Запитання 6

Знайдіть log5125

варіанти відповідей

 

25

 

 

3

 

 

5

 

 

15

Запитання 7

Знайдіть log42

варіанти відповідей

 

¼

 

 

√2

 

 

½

 

 

⅛

Запитання 8

Обчисліть lg4+lg25

варіанти відповідей

 

100

 

 

3

 

 

2

 

 

10

Запитання 9

Обчисліть log217+log213

варіанти відповідей

 

1

 

 

10

 

 

4

 

 

52